Nth Dimension Sudoku Solver

Tags: Java, recursion, backtracking, data structures and algorithms

This is a sudoku program I programmed in Java that is capable of solving any sudoku problem of any given dimension. It can solve the classic 9x9 sudoku board or even the 50x50 sudoku board if you so choose. It comes complete with J Unit testing implemented and a few demo problems and examples to help you get started. You can find the github repository here or you can download it yourself here.

Guide

The program reads text files as input with the first number being the dimensions of the sudoku board and the periods representing unknown tiles. You can create this text file by copying what you see on the board then feeding it to the program. It will then tell you the first solution it finds, or tell you that the puzzle is unsolvable.

Here is an example of how your input file should look

Technical Details

The time and space complexity of this program is O(n^n) where n is the dimensions of the puzzle which does sound worrying, but by taking advantage of backtracking and recursive techniques, this time is greatly reduced but is not reflected in big O notation. The puzzle is solved by creating a 2D array to store the current working solution the program is developing. The program works by creating a tree structure with every possible solution. The program however only works on one branch at a time which greatly improves performance. The program navigates the tree using post order tree traversal.

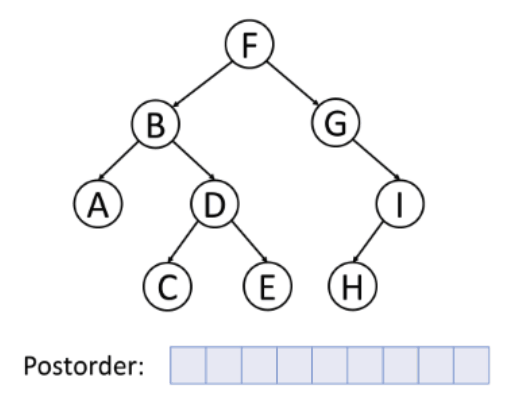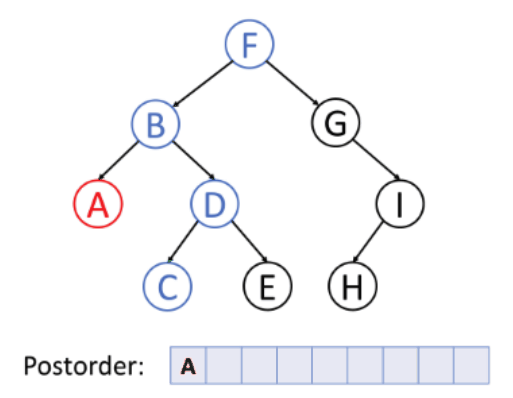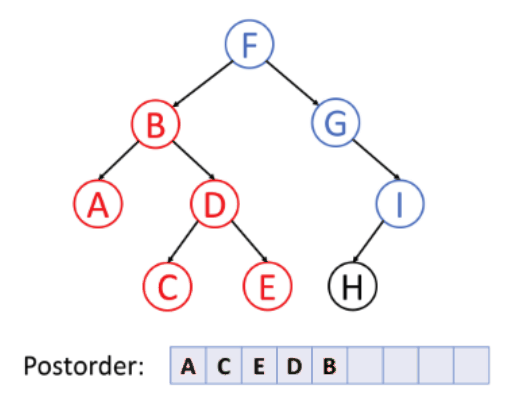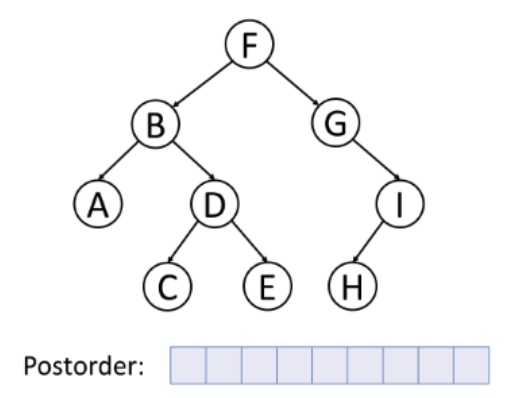
GIF source:

https://commons.wikimedia.org/wiki/File:Postorder-traversal.gif

The program goes through the sudoku problem trying a new number in each unfilled slot. After every new number, a battery of tests are used to make sure the number is legal. If it isn't, it backtracks to a previous branch in post order by using recursion. This process is repeated unti there are no more branches meaning there is no solution, or until the end of the 2D array is reached meaning there is a solution.